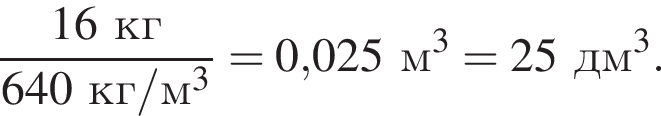При спуске в шахту на каждые 12 м атмосферное давление возрастает на 1 мм рт. ст. Если на поверхности Земли барометр показывает давление p1 = 760 мм рт. ст., то в шахте на глубине h = 360 м давление p2 равно:
Вблизи поверхности Земли атмосферное давление убывает на 133 Па при подъёме на каждые 12 м. Если у подножия горы, высота которой h = 288 м, атмосферное давление p1 = 101,3 кПа, то на её вершине давление p2 равно:
Вблизи поверхности Земли атмосферное давление убывает на 1 мм рт. ст. при подъеме на каждые 12 м. Если у подножия атмосферное давление p1 = 760 мм рт. ст., а на ее вершине p2 = 732 мм рт. ст., то высота h горы равна:
При спуске в шахту на каждые 12 м атмосферное давление возрастает на 1 мм рт. ст. Если на поверхности Земли барометр показывает давление p1 = 760 мм рт. ст., а на дне шахты — p2 = 792 мм рт. ст., то глубина h шахты равна:
Лифт начал подниматься с ускорением, модуль которого a = 1,2 м/с2. В некоторый момент c потолка кабины лифта оторвался болт. Если высота кабины h = 2,4 м, а болт переместился относительно поверхности Земли за время его движения в лифте вертикально вверх на Δr = 80 см, то модуль скорости V движения лифта в момент отрыва болта равен ... дм/с.
Камень бросили горизонтально с некоторой высоты со скоростью, модуль которой υ0 = 20 м/с. Через промежуток времени Δt = 3 с от момента броска модуль скорости камня υ будет равен:
Тело, брошенное вертикально вниз с некоторой высоты, за последние две секунды движения прошло путь  Если модуль начальной скорости тела
Если модуль начальной скорости тела 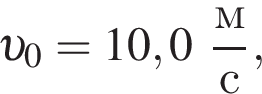 то высота h равна:
то высота h равна:
С башни в горизонтальном направлении бросили тело с начальной скоростью, модуль которой υ0 = 6 м/с. Через промежуток времени Δt = 0,8 с после момента броска модуль скорости υ тела в некоторой точке траектории будет равен:
На гладкой горизонтальной поверхности лежит брусок массой m1, прикрепленный к стене невесомой пружиной жесткостью
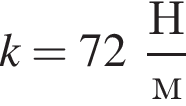 (см.рис.). Пластилиновый шарик массой
(см.рис.). Пластилиновый шарик массой  летящий горизонтально вдоль оси пружины со скоростью, модуль которой
летящий горизонтально вдоль оси пружины со скоростью, модуль которой 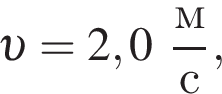 попадает в брусок и прилипает к нему. Если максимальное сжатие пружины
попадает в брусок и прилипает к нему. Если максимальное сжатие пружины  то масса m1 бруска равна ... г.
то масса m1 бруска равна ... г.
Металлический шарик падает вертикально вниз на горизонтальную поверхность стальной плиты со скоростью, модуль которой 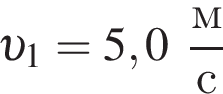 и отскакивает от нее вертикально вверх с такой же по модулю скоростью:
и отскакивает от нее вертикально вверх с такой же по модулю скоростью:  Если масса шарика
Если масса шарика 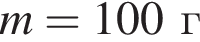 то модуль изменения импульса
то модуль изменения импульса ![]() шарика при ударе о плиту равен:
шарика при ударе о плиту равен:
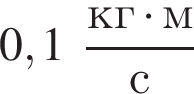
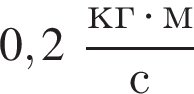
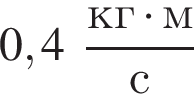

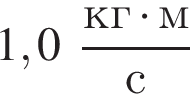
Шайба массой  подлетела к вертикальному борту хоккейной коробки и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним:
подлетела к вертикальному борту хоккейной коробки и отскочила от него в противоположном направлении со скоростью, модуль которой остался прежним:  Если модуль изменения импульса шайбы
Если модуль изменения импульса шайбы 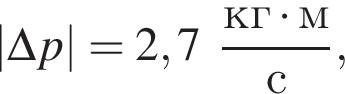 то модуль скорости шайбы υ2 непосредственно после ее удара о борт равен:
то модуль скорости шайбы υ2 непосредственно после ее удара о борт равен:
Два тела массами m1 = 6,00 кг и m2 = 8,00 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 10,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Два тела массами m1 = 4,00 кг и m2 = 3,00 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 15,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Два тела массами m1 = 2,00 кг и m2 = 1,50 кг, модули скоростей которых одинаковы (υ1 = υ2), двигались по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях. Если после столкновения тела движутся как единое целое со скоростью, модуль которой u = 5,0 м/с, то количество теплоты Q, выделившееся при столкновении, равно ... Дж.
Диаметр велосипедного колеса d = 66 см, число зубьев ведущей звездочки N1 = 44, ведомой — N2 = 14 (см. рис.). Если велосипедист равномерно крутит педали с частотой ν = 82 об/мин, то модуль скорости V велосипеда равен ... км/ч.
Тонкий стержень с закрепленными на его концах небольшими бусинками 1 и 2 равномерно вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через точку О (см. рис.). Если первая бусинка находится на расстоянии r1 = 25 см от оси вращения, а модули линейной скорости второй и первой бусинок отличаются в k = 3,0 раза, то длина l стержня равна:
Автомобиль движется по дороге со скоростью, модуль которой 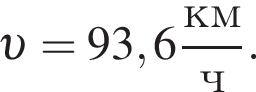 Профиль дороги показан на рисунке. В точке С радиус кривизны профиля R = 255 м. Если в точке С, направление на которую из центра кривизны составляет с вертикалью угол
Профиль дороги показан на рисунке. В точке С радиус кривизны профиля R = 255 м. Если в точке С, направление на которую из центра кривизны составляет с вертикалью угол  модуль силы давления автомобиля на дорогу F = 5,16 кН, то масса m автомобиля равна ... кг.
модуль силы давления автомобиля на дорогу F = 5,16 кН, то масса m автомобиля равна ... кг.
Материальная точка движется равномерно по окружности радиусом R = 19 см со скоростью, модуль которой υ = 1,9 м/с. Радиус-вектор, проведённый из центра окружности к материальной точке, повернётся на угол  рад за промежуток времени
рад за промежуток времени ![]() равный:
равный:
Два соединенных между собой вертикальных цилиндра заполнены несжимаемой жидкостью и закрыты невесомыми поршнями, которые могут перемещаться без трения. К поршням приложены силы
![]() и
и ![]() направления которых указаны на рисунке. Если модуль силы F2 = 18 Н, то для удержания системы в равновесии модуль силы F1 должен быть равен:
направления которых указаны на рисунке. Если модуль силы F2 = 18 Н, то для удержания системы в равновесии модуль силы F1 должен быть равен:
На рисунке изображён график зависимости гидростатического давления p от глубины h для жидкости, плотность
![]() которой равна:
которой равна:
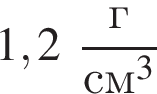
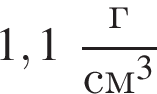
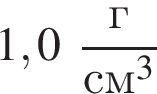
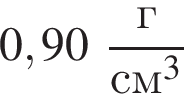
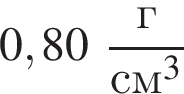
В нижней части сосуда, заполненного газом, находится скользящий без трения невесомый поршень (см.рис.). Для удержания поршня в равновесии к нему приложена внешняя сила
![]() Направление силы давления газа, действующей на плоскую стенку AB сосуда, указано стрелкой, номер которой:
Направление силы давления газа, действующей на плоскую стенку AB сосуда, указано стрелкой, номер которой:
В нижней части сосуда, заполненного газом, находится скользящий без трения невесомый поршень (см.рис.). Для удержания поршня в равновесии к нему приложена внешняя сила
![]() Направление силы давления газа, действующей на плоскую стенку AB сосуда, указано стрелкой, номер которой:
Направление силы давления газа, действующей на плоскую стенку AB сосуда, указано стрелкой, номер которой:
Запаянную с одного конца трубку наполнили маслом (
 ), а затем погрузили открытым концом в широкий сосуд с маслом (см.рис.). Если высота столба масла h = 10,5 м, то атмосферное давление p равно:
), а затем погрузили открытым концом в широкий сосуд с маслом (см.рис.). Если высота столба масла h = 10,5 м, то атмосферное давление p равно:
Запаянную с одного конца трубку наполнили соляным раствором (
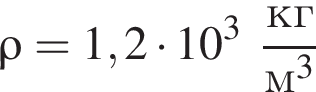 ), а затем погрузили открытым концом в широкий сосуд с соляным раствором (см.рис.). Если высота столба соляного раствора h = 8,50 м, то атмосферное давление p равно:
), а затем погрузили открытым концом в широкий сосуд с соляным раствором (см.рис.). Если высота столба соляного раствора h = 8,50 м, то атмосферное давление p равно:
Запаянную с одного конца трубку наполнили керосином (
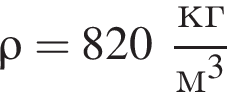 ), а затем погрузили открытым концом в широкий сосуд с керосином (см.рис.). Если высота столба керосина h = 12,2 м, то атмосферное давление p равно:
), а затем погрузили открытым концом в широкий сосуд с керосином (см.рис.). Если высота столба керосина h = 12,2 м, то атмосферное давление p равно:
В нижней части сосуда, заполненного газом, находится скользящий без трения невесомый поршень (см.рис.). Для удержания поршня в равновесии к нему приложена внешняя сила
![]() Направление силы давления газа, действующей на плоскую стенку AB сосуда, указано стрелкой, номер которой:
Направление силы давления газа, действующей на плоскую стенку AB сосуда, указано стрелкой, номер которой:
На рисунке изображён график зависимости гидростатического давления p от глубины h для жидкости, плотность
![]() которой равна:
которой равна:
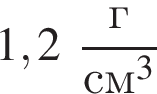
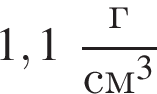
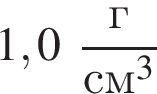
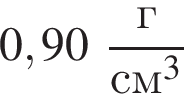
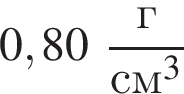
На рисунке изображён график зависимости гидростатического давления p от глубины h для жидкости, плотность
![]() которой равна:
которой равна:
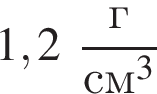
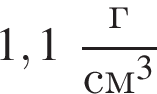
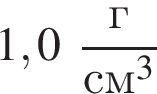
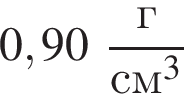
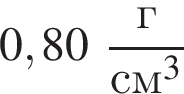
В двух вертикальных сообщающихся сосудах находится ртуть (![]() 1 = 13,6 г/см3). Поверх ртути в один сосуд налили слой воды (
1 = 13,6 г/см3). Поверх ртути в один сосуд налили слой воды (![]() 2 = 1,00 г/см3) высотой H = 23 см. Разность
2 = 1,00 г/см3) высотой H = 23 см. Разность ![]() h уровней ртути в сосудах равна:
h уровней ртути в сосудах равна:
Звуковой сигнал, посланный эхолокатором в момент времени t1 = 0 c, отразился от препятствия, возвратился обратно в момент времени t2 = 2,66 с. Если модуль скорости распространения звука в воздухе υ = 340 м/с, то расстояние L от локатора до препятствия равно:
Мальчик крикнул, и эхо, отражённое от преграды, возвратилось к нему обратно через промежуток времени Δt = 1,2 с. Если модуль скорости звука в воздухе υ = 0,330 км/с, то расстояние L от мальчика до преграды равно:
Подъемный кран движется равномерно в горизонтальном направлении со скоростью, модуль которой относительно поверхности Земли υ = 80 cм/с, и одновременно поднимает вертикально груз со скоростью, модуль которой относительно стрелы крана u = 60 cм/с . Модуль перемещения ![]() r груза относительно поверхности Земли за промежуток времени
r груза относительно поверхности Земли за промежуток времени ![]() t = 1,5 мин равен:
t = 1,5 мин равен:
Тело движется равноускоренно в положительном направлении оси Ox. В момент начала отсчёта времени t0 = 0 c проекция скорости тела υ0x = 4,0 м/c. Если проекция ускорения тела на ось ах = 4,0, то проекция перемещения ∆rх тела за шестую секунду равна ... м.
На рисунке представлены фотографии электромобиля, сделанные через равные промежутки времени Δt = 1,2 c. Если электромобиль двигался прямолинейно и равноускоренно, то в момент времени, когда был сделан второй снимок, проекция скорости движения электромобиля υx на ось Ox была равна ... км/ч.
Проекция скорости движения тела υx на ось Ox зависит от времени t согласно закону υx = A + Bt, где A = 8 м/с, B = 4 м/с2. Этой зависимости соответствует график (см. рис.), обозначенный буквой:
Тело массой m = 100 г свободно падает без начальной скорости с высоты h над поверхностью Земли. Если на высоте h1 = 6,0 м кинетическая энергия тела Eк = 12 Дж, то высота h равна ... м.
Масса m1 первого тела в два раза больше массы m2 второго тела. Если модули скоростей этих тел равны (υ1 = υ2), то отношение кинетической энергии первого тела к кинетической энергии второго тела ![]() равно:
равно:
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 10 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 100 пКл) шарик массой m = 380 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 100 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 100 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Два маленьких шарика массами m1 = 24 г и m2 = 12 г подвешены на невесомых нерастяжимых нитях одинаковой длины l = 63 см так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота hmax, на которую они поднялись, равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота hmax, на которую они поднялись, равна … см.
На рисунке изображены три положения груза пружинного маятника, совершающего свободные незатухающие колебания с амплитудой x0. Если в положении В полная механическая энергия маятника W = 8,0 Дж, то в положении Б она равна:
Модуль скорости υ1 первого тела в два раза больше модуля скорости движения υ2 второго тела. Если массы этих тел равны 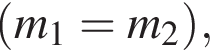 то отношение кинетической энергии первого тела к кинетической энергии второго тела
то отношение кинетической энергии первого тела к кинетической энергии второго тела ![]() равно:
равно:
На невесомой нерастяжимой нити длиной l = 72 см висит небольшой шар массой М = 43,6 г. Пуля массой m = 2,4 г, летящая горизонтально со скоростью ![]() попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
попадает в шар и застревает в нем. Если скорость пули была направлена вдоль диаметра шара, то шар совершит полный оборот по окружности в вертикальной плоскости при минимальном значении скорости υ0 пули, равном ...м/с .
С некоторой высоты h в горизонтальном направлении бросили камень, траектория полёта которого показана штриховой линией (см. рис.). Если в точке Б полная механическая энергия камня W = 12,0 Дж, то в точке А после броска она равна:
Тело свободно падает без начальной скорости с высоты h = 20 м над поверхностью Земли. Если масса тела m = 200 г, то на высоте h1 = 8,0 м кинетическая энергия Eк тела равна ... Дж.
Камень бросили вертикально вверх с поверхности Земли со скоростью, модуль которой 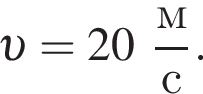 Кинетическая энергия камня равна его потенциальной на высоте h, равной ... м.
Кинетическая энергия камня равна его потенциальной на высоте h, равной ... м.
Два маленьких шарика массами m1 = 16 г и m2 = 8 г подвешены на невесомых нерастяжимых нитях одинаковой длины l так, что поверхности шариков соприкасаются. Первый шарик сначала отклонили таким образом, что нить составила с вертикалью угол  а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись, hmax = 6,0 см, то длина l нити равна … см.
а затем отпустили без начальной скорости. Если после неупругого столкновения шарики стали двигаться как единое целое и максимальная высота, на которую они поднялись, hmax = 6,0 см, то длина l нити равна … см.
Две вертикальные однородно заряженные непроводящие пластины расположены в вакууме на расстоянии d = 80 мм друг от друга. Между пластинами на длинной лёгкой нерастяжимой нити подвешен небольшой заряженный (|q0| = 500 пКл) шарик массой m = 380 мг, который движется, поочерёдно ударяясь о пластины. При ударе о каждую из пластин шарик теряет ![]() = 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 250 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
= 19,0 % своей кинетической энергии. В момент каждого удара шарик перезаряжают, и знак его заряда изменяется на противоположный. Если модуль напряжённости однородного электростатического поля между пластинами E = 250 кВ/м, то период T ударов шарика об одну из пластин равен ... мс.
Фотоэлектроны, выбиваемые с поверхности металла светом с длиной волны λ = 330 нм, полностью задерживаются, когда разность потенциалов между электродами фотоэлемента Uз = 1,76 В. Длина волны λк, соответствующая красной границе фотоэффекта, равна:
Если работа выхода электрона с поверхности вольфрама  составляет
составляет ![]() часть от энергии падающего фотона, то максимальная кинетическая энергия
часть от энергии падающего фотона, то максимальная кинетическая энергия ![]() фотоэлектрона равна ... эВ.
фотоэлектрона равна ... эВ.
Если при облучении фотонами металла, для которого работа выхода Aвых = 3 эВ, максимальная кинетическая энергия фотоэлектронов ![]() = 8 эВ, то энергия фотонов E равна:
= 8 эВ, то энергия фотонов E равна:
Если работа выхода электрона с поверхности цезия Aвых = 3,0 · 10-19 Дж, а энергия фотона, падающего на этот металл, E = 5,0 эВ, то максимальная кинетическая энергия ![]() фотоэлектрона равна:
фотоэлектрона равна:
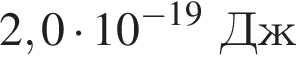
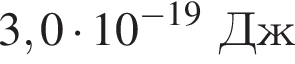
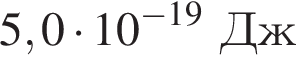
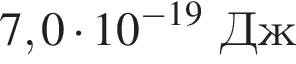
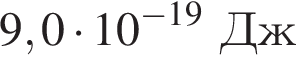
Если работа выхода электрона с поверхности цезия Aвых = 2,4 эВ, а максимальная кинетическая энергия фотоэлектрона ![]() = 4 · 10-19 Дж, то энергияE фотона, падающего на поверхность металла, равна:
= 4 · 10-19 Дж, то энергияE фотона, падающего на поверхность металла, равна:
Если работа выхода электрона с поверхности металла Aвых = 4,1 · 10-19 Дж, а максимальная кинетическая энергия фотоэлектрона ![]() = 2,4 · 10-19 Дж, то длина волны λ монохроматического света, падающего на поверхность металла, равна:
= 2,4 · 10-19 Дж, то длина волны λ монохроматического света, падающего на поверхность металла, равна:
Если работа выхода электрона с поверхности цинка 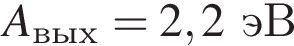 составляет
составляет ![]() часть от энергии падающего фотона, то максимальная кинетическая энергия
часть от энергии падающего фотона, то максимальная кинетическая энергия ![]() фотоэлектрона равна ... эВ.
фотоэлектрона равна ... эВ.
К источнику переменного тока, напряжение на клеммах которого изменяется по гармоническому закону, подключена электрическая плитка, потребляющая мощность Р = 560 Вт. Если действующее значение напряжения на плитке Uд = 72 В, то амплитудное значение силы тока I0 в сети равно … А.
Электрический нагреватель подключен к электрической сети, напряжение в которой изменяется по гармоническому закону. Амплитудное значение напряжения в сети U0 = 151 В. Если действующее значение силы тока в цепи Iд = 0,33 А, то нагреватель потребляет мощность P, равную ... Вт.
Напряжение на участке цепи изменяется по гармоническому закону (см. рис.). В момент времени tА = 15 мс напряжение на участке цепи равно UА, а в момент времени tB = 40 мс равно UB. Если разность напряжений UA − UB = 50 В, то действующее значение напряжения Uд равно ... В.
К источнику переменного тока, напряжение на клеммах которого изменяется по гармоническому закону, подключена электрическая плитка, потребляющая мощность Р = 840 Вт. Если действующее значение напряжения на плитке Uд = 59 В, то амплитудное значение силы тока I0 в сети равно … А.
На рисунке 1 изображен участок электрической цепи, на котором параллельно катушке индуктивности L включена лампочка Л. График зависимости силы тока I в катушке индуктивности от времени t показан на рисунке 2. Лампочка будет светить наиболее ярко в течение интервала времени:
Сила тока в катушке индуктивности равномерно уменьшилась от I1 = 4,0 А до I2 = 0,0 А за промежуток времени 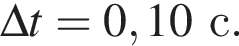 Если в катушке возникла ЭДС самоиндукции
Если в катушке возникла ЭДС самоиндукции 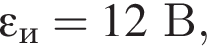 то индуктивность катушки L равна:
то индуктивность катушки L равна:
Электрический нагреватель подключен к электрической сети, напряжение в которой изменяется по гармоническому закону. Амплитудное значение напряжения в сети U0 = 69 В. Если действующее значение силы тока в цепи Iд = 0,70 А, то нагреватель потребляет мощность P, равную ... Вт.
Цилиндр плавает в воде
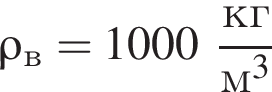 в вертикальном положении (см.рис.). Если масса цилиндра m = 10 кг, то объем V цилиндра равен … дм3.
в вертикальном положении (см.рис.). Если масса цилиндра m = 10 кг, то объем V цилиндра равен … дм3.
Деревянный шар (![]() = 4,0 · 102 кг/м3) всплывает в воде (
= 4,0 · 102 кг/м3) всплывает в воде (![]() = 1,0 · 103 кг/м3) с постоянной скоростью. Отношение
= 1,0 · 103 кг/м3) с постоянной скоростью. Отношение ![]() модулей силы сопротивления воды и силы тяжести, действующих на шар, равно:
модулей силы сопротивления воды и силы тяжести, действующих на шар, равно:
Цилиндр плавает в воде
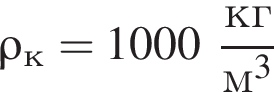 в вертикальном положении (см.рис.). Если масса цилиндра m = 27 кг, то объем V цилиндра равна … дм3.
в вертикальном положении (см.рис.). Если масса цилиндра m = 27 кг, то объем V цилиндра равна … дм3.
Шар, изготовленный из сосны (![]() = 5,0 · 102 кг/м3) всплывает в воде (
= 5,0 · 102 кг/м3) всплывает в воде (![]() = 1,0 · 103 кг/м3) с постоянной скоростью. Если объем шара V = 1,0 дм3, то модуль силы сопротивления Fс воды движению шара равен:
= 1,0 · 103 кг/м3) с постоянной скоростью. Если объем шара V = 1,0 дм3, то модуль силы сопротивления Fс воды движению шара равен:
Небольшой пузырёк воздуха медленно поднимается вверх со дна водоёма. На глубине h1 = 80 м температура воды (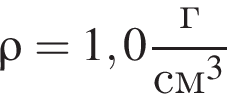 )
) 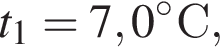 а объём пузырька V1. Если атмосферное давление
а объём пузырька V1. Если атмосферное давление 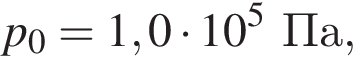 то на глубине h2 = 2,0 м, где температура воды
то на глубине h2 = 2,0 м, где температура воды 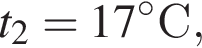 на пузырёк действует выталкивающая сила, модуль которой F2 = 3,5 мН, то объем пузырька V1 был равен … мм3.
на пузырёк действует выталкивающая сила, модуль которой F2 = 3,5 мН, то объем пузырька V1 был равен … мм3.
Цилиндр плавает в керосине
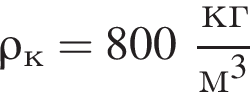 в вертикальном положении (см.рис.). Если объем цилиндра V = 0,030 м3, то масса m цилиндра равна … кг.
в вертикальном положении (см.рис.). Если объем цилиндра V = 0,030 м3, то масса m цилиндра равна … кг.
Цилиндр плавает в бензине
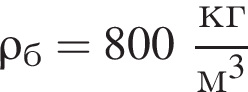 в вертикальном положении (см. рис.). Если масса цилиндра m = 16 кг, то объем V цилиндра равен … дм3.
в вертикальном положении (см. рис.). Если масса цилиндра m = 16 кг, то объем V цилиндра равен … дм3.

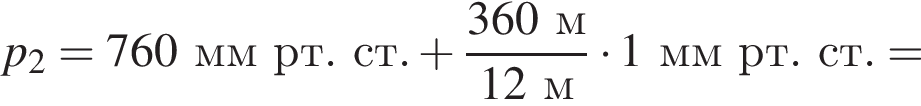
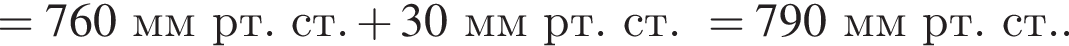

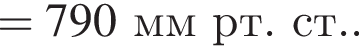
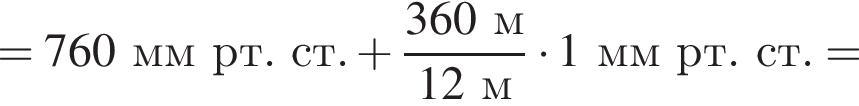
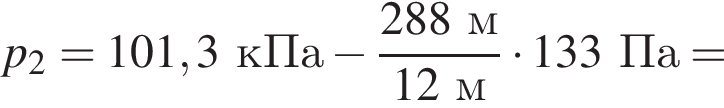

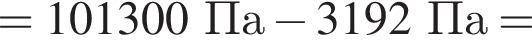

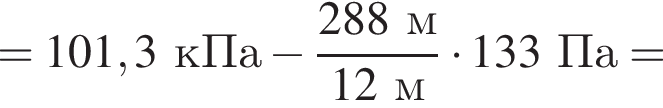
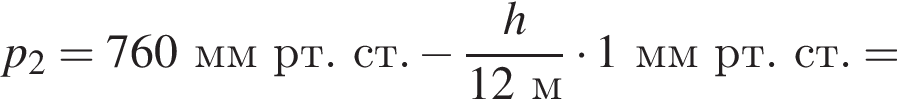

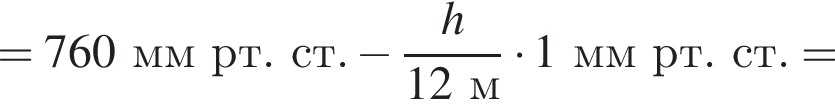
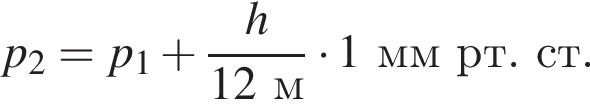
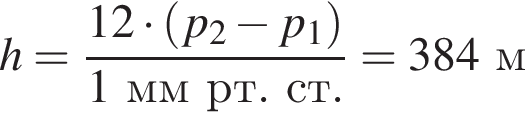
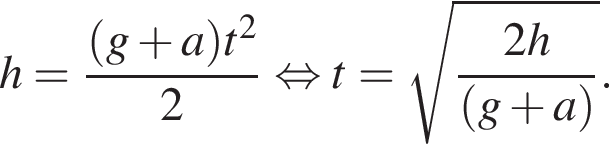
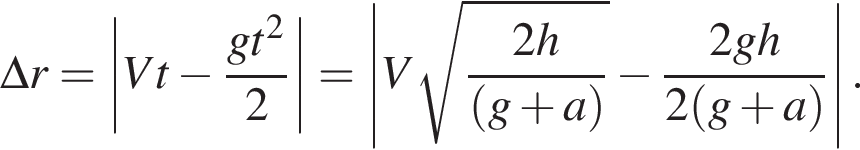
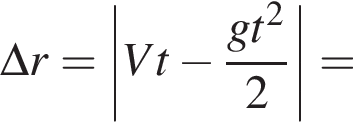
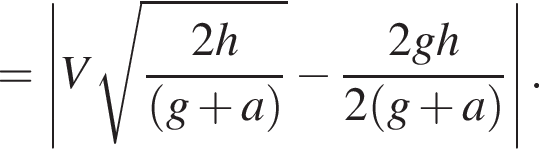
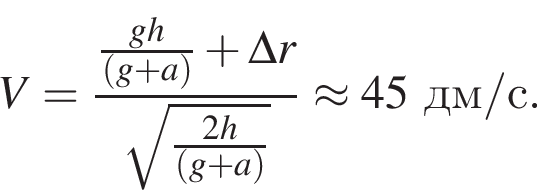
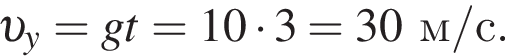 Горизонтальная составляющая скорости оставалась постоянной
Горизонтальная составляющая скорости оставалась постоянной 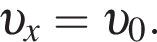 Модуль скорости камня равен
Модуль скорости камня равен 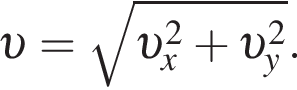 Таким образом, получаем
Таким образом, получаем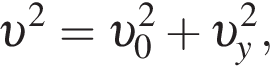
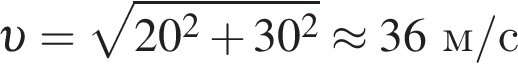
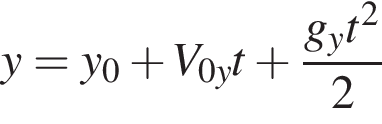

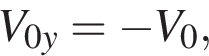
 значит,
значит,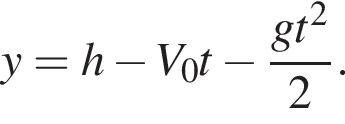
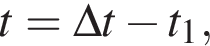
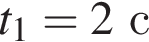 уравнение движения примет вид:
уравнение движения примет вид: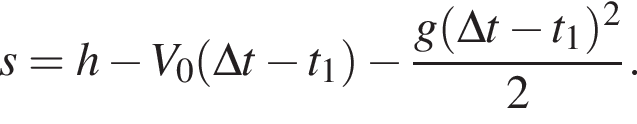
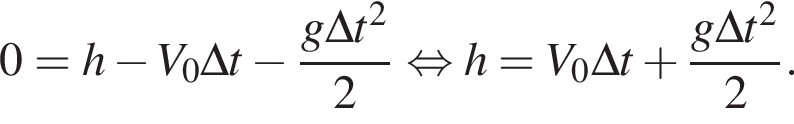
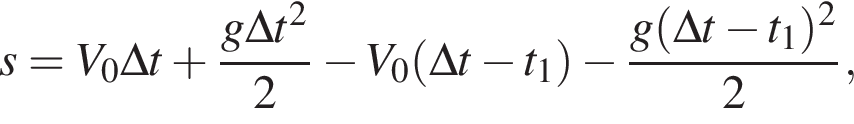
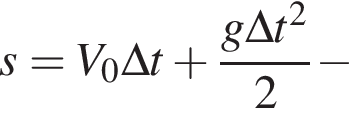
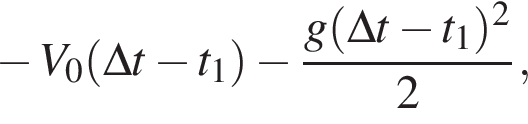
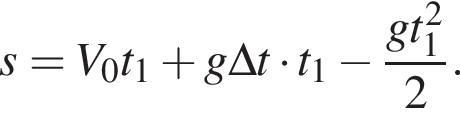
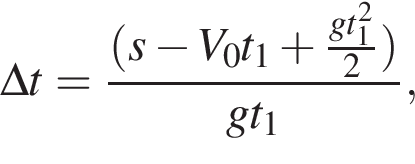
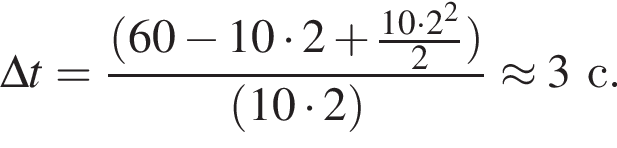
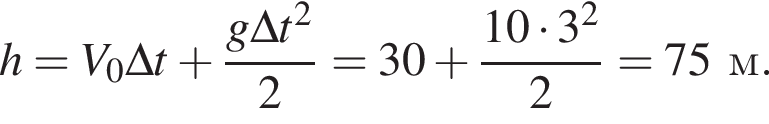
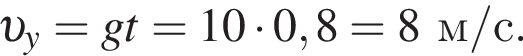 Горизонтальная составляющая скорости оставалась постоянной
Горизонтальная составляющая скорости оставалась постоянной 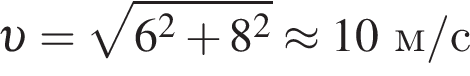
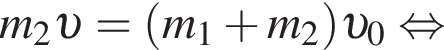
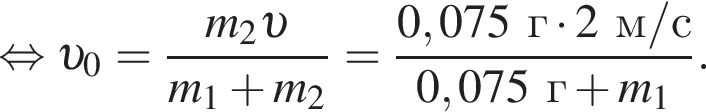
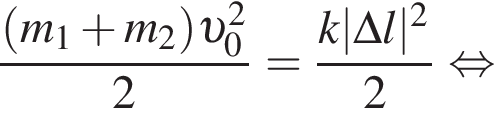
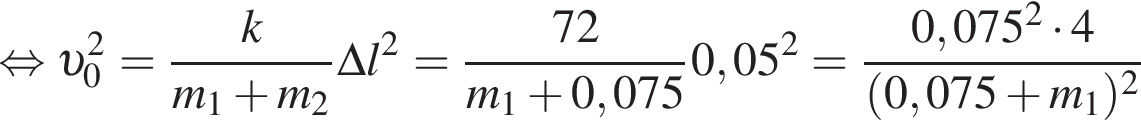
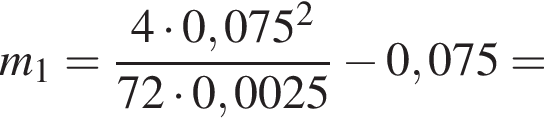



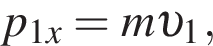
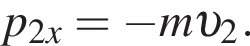
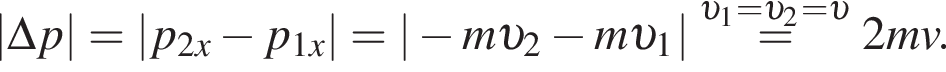
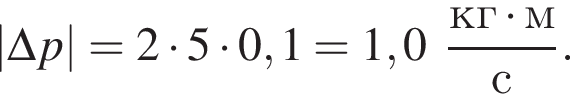
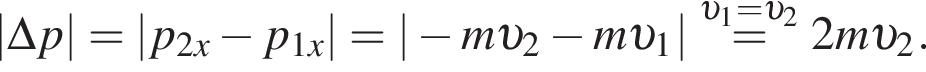
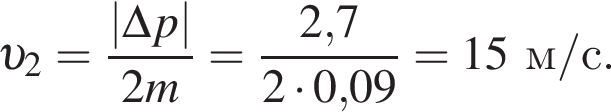
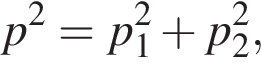
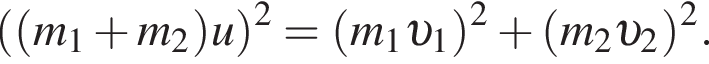
 получаем:
получаем: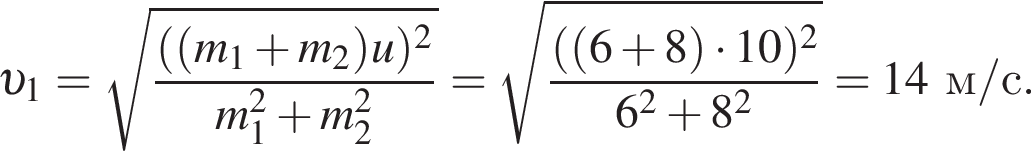
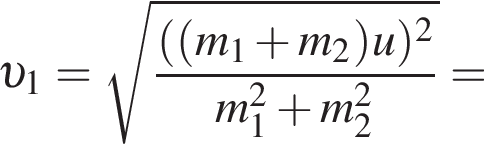
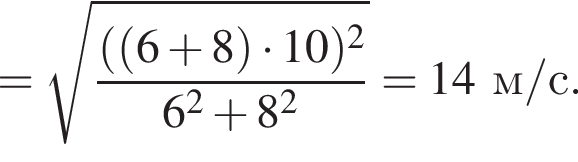
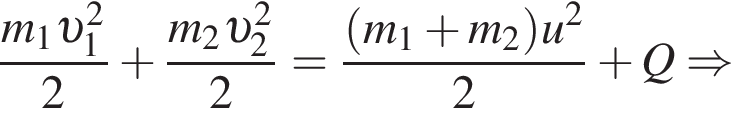
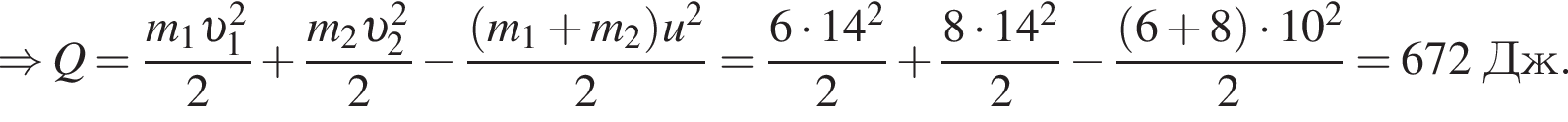
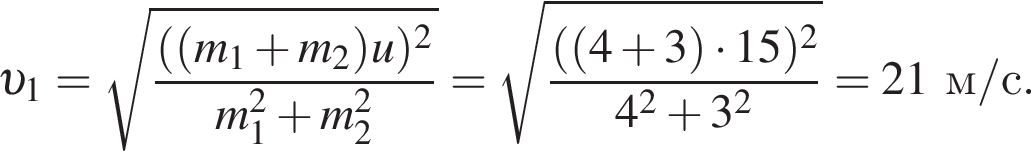
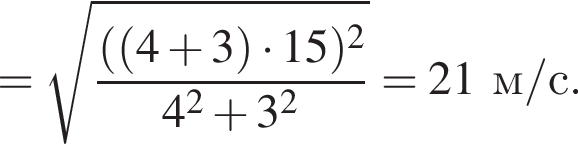
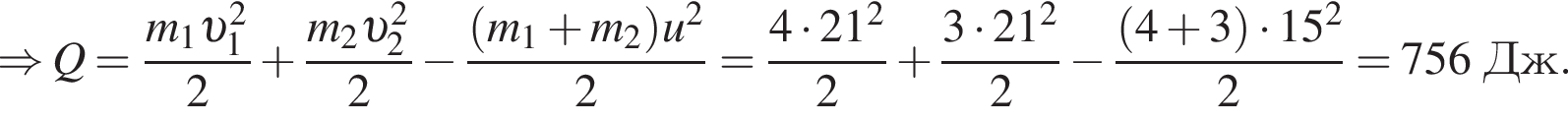
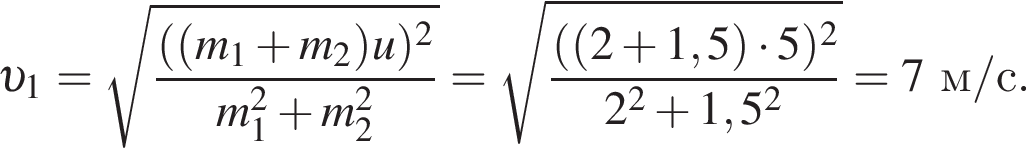
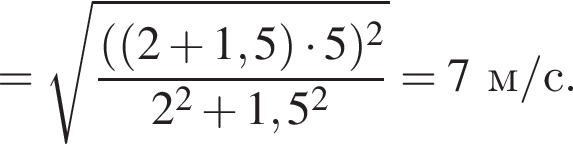
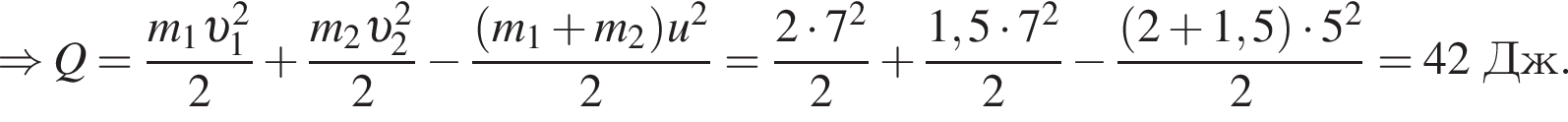
 где k — коэффициент пропорциональности. Выражая отсюда радиусы 1-ой и 2-ой звёздочек, получаем:
где k — коэффициент пропорциональности. Выражая отсюда радиусы 1-ой и 2-ой звёздочек, получаем: 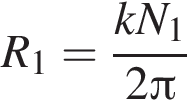 и
и 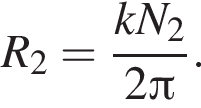
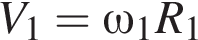 и
и 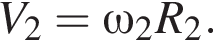 Угловая частота вращения первой звездочки с частотой вращения педалей связана выражением:
Угловая частота вращения первой звездочки с частотой вращения педалей связана выражением: 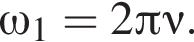
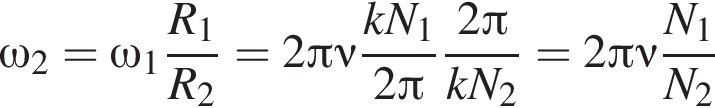
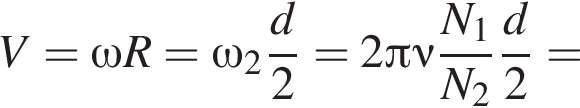
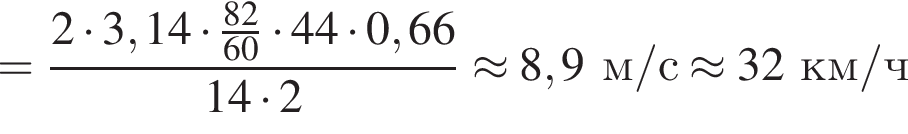
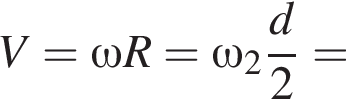
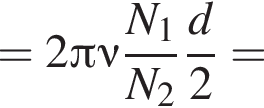
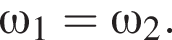
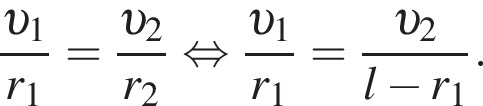
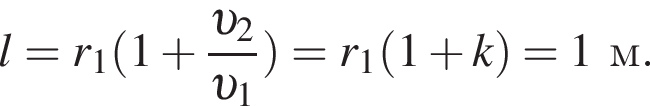
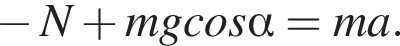 Центростремительное ускорение равно:
Центростремительное ускорение равно: 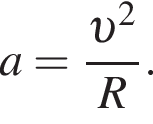 N = F по третьему закону Ньютона.
N = F по третьему закону Ньютона.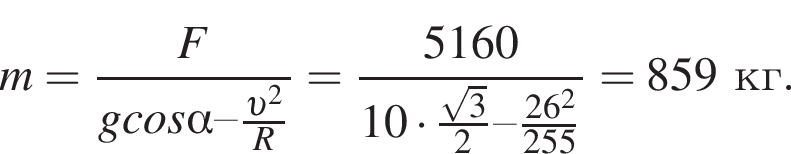
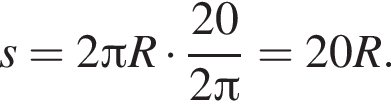
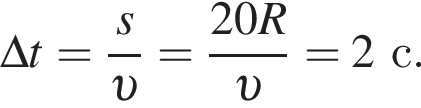

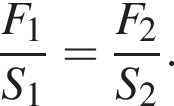
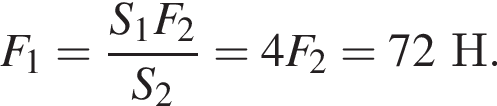
 Плотность можно определить, взяв любую точку из графика, например (60 см, 4,8 кПа):
Плотность можно определить, взяв любую точку из графика, например (60 см, 4,8 кПа):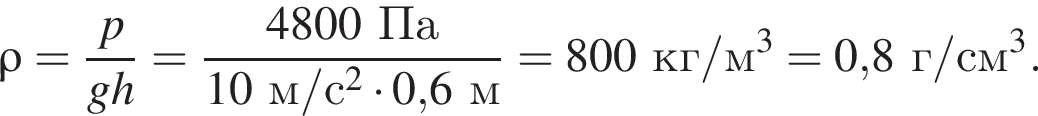
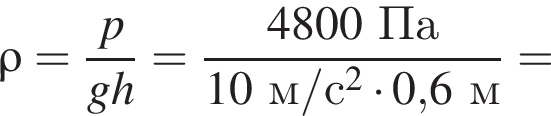
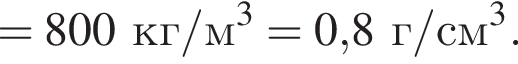

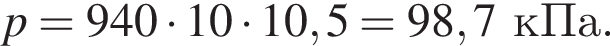
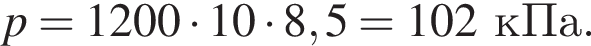
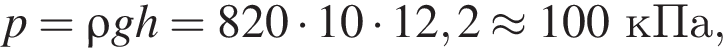
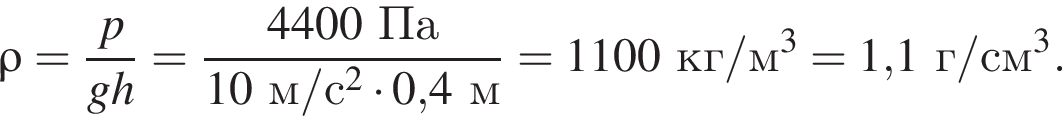
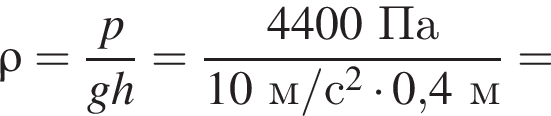
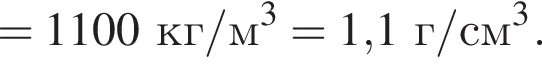
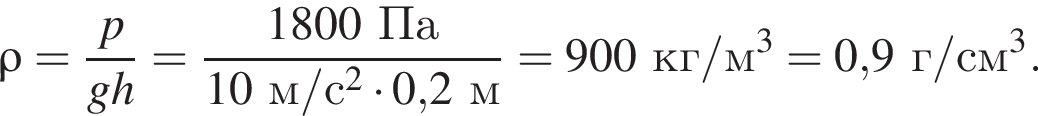
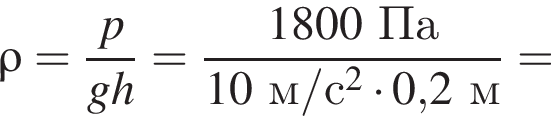
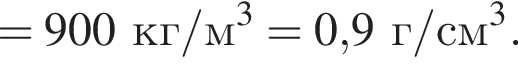

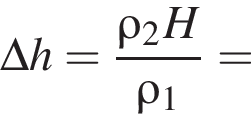

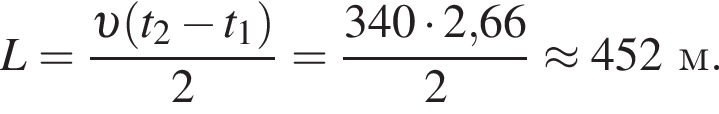
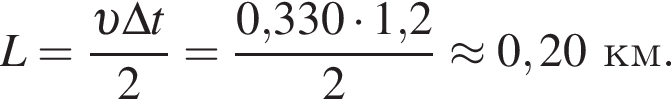

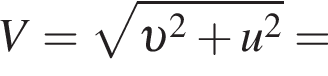
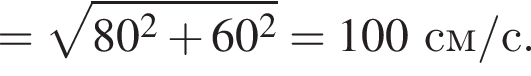



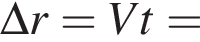
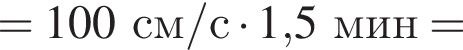
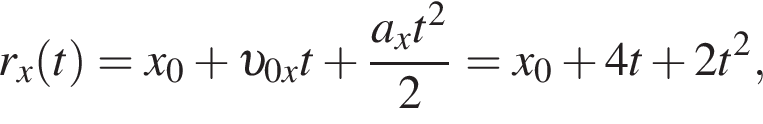 где
где 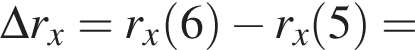
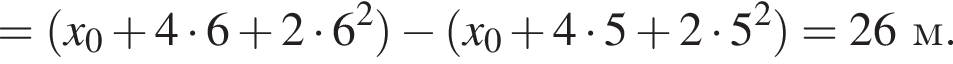


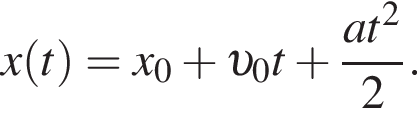
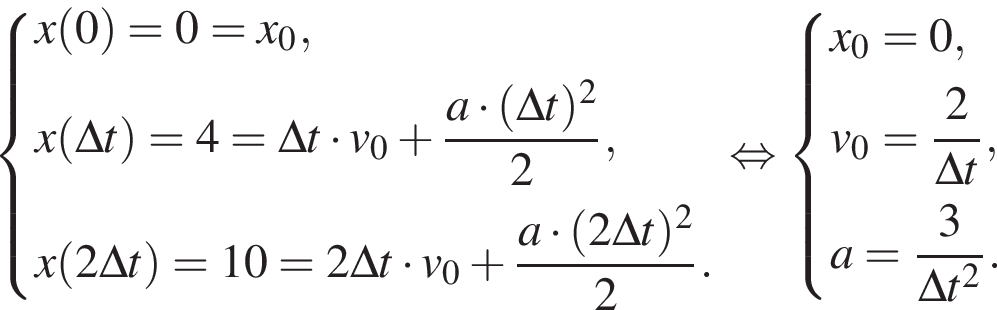
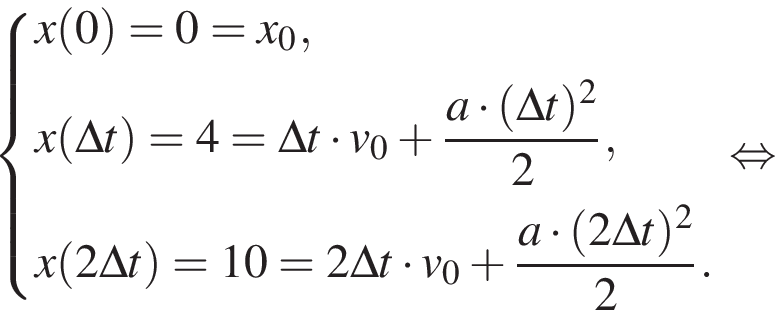
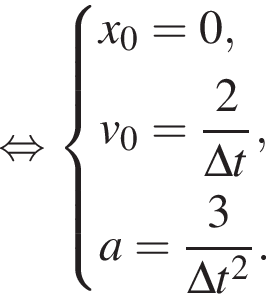
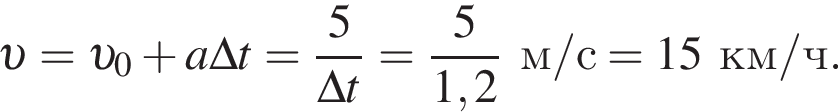
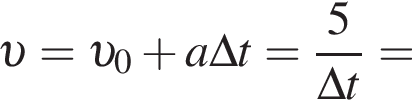
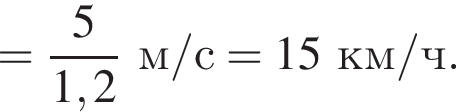
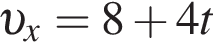 соответствует график под буквой б.
соответствует график под буквой б.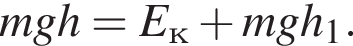
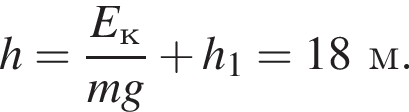
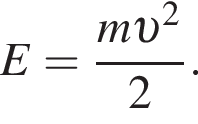 По условию
По условию 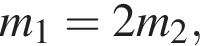 значит,
значит,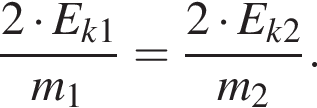
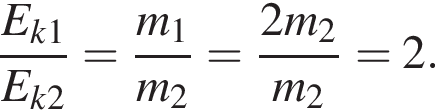
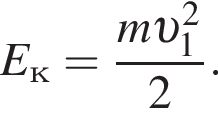 В электрическом поле шарик разгоняется, увеличивая свою кинетическую энергию на
В электрическом поле шарик разгоняется, увеличивая свою кинетическую энергию на  В установившемся режиме после соударения с противоположной пластиной кинетическая энергия шарика уменьшается до исходного значения
В установившемся режиме после соударения с противоположной пластиной кинетическая энергия шарика уменьшается до исходного значения 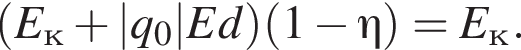
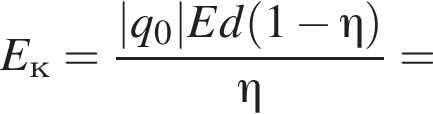
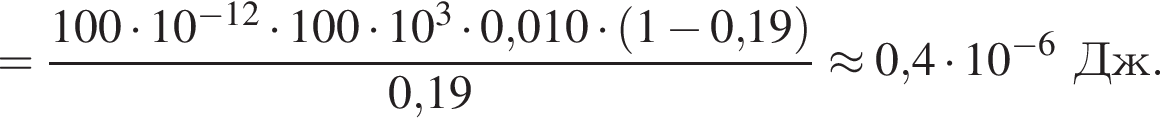
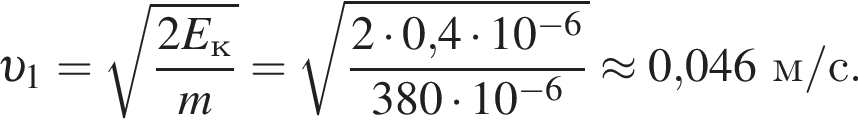
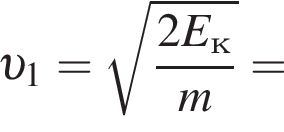
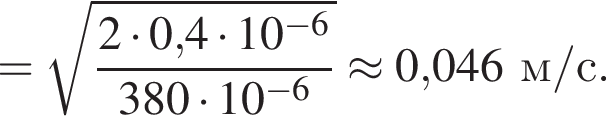
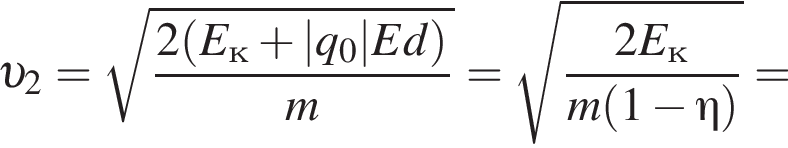
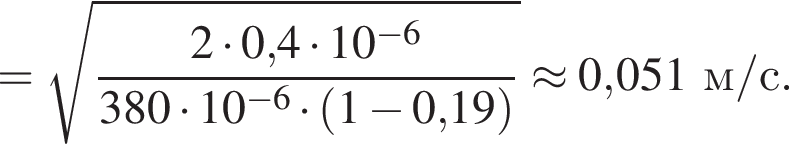
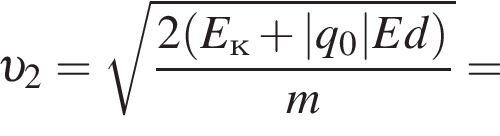
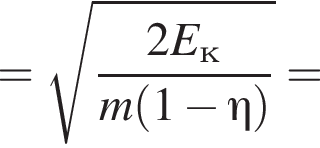
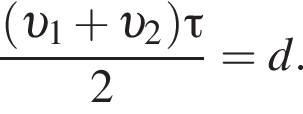
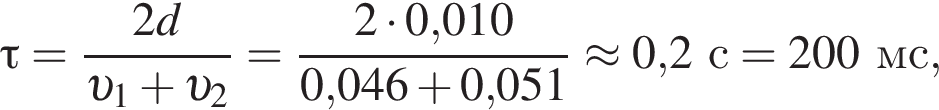
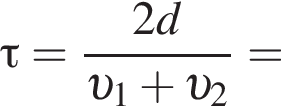
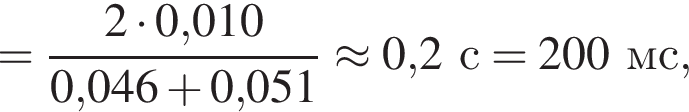
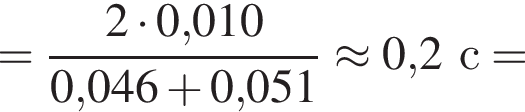
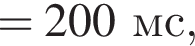

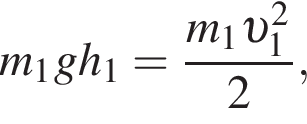
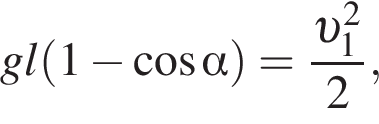
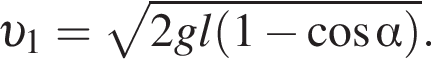

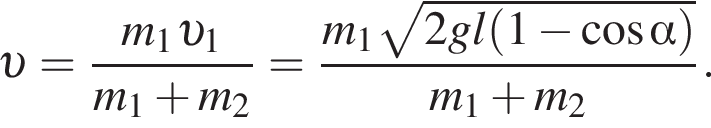
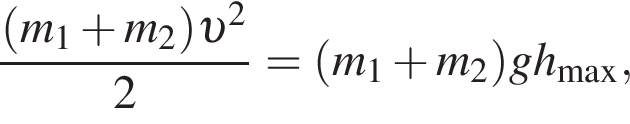
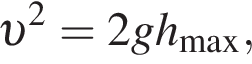
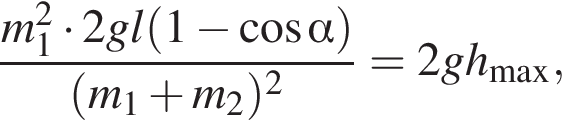
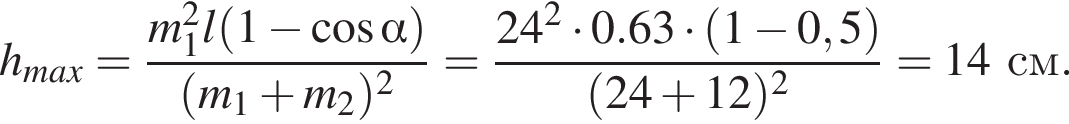
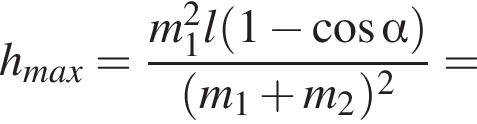
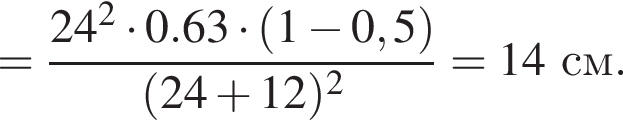
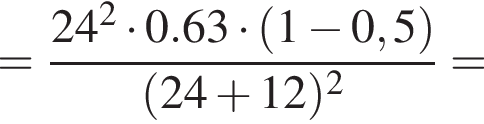
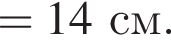
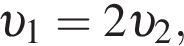
 значит
значит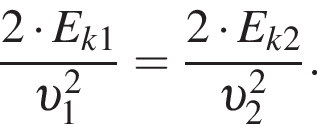
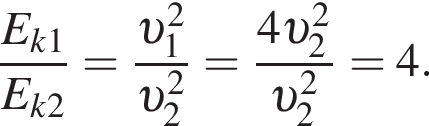

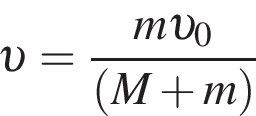 — скорость системы "пуля+шар" после застревания пули.
— скорость системы "пуля+шар" после застревания пули.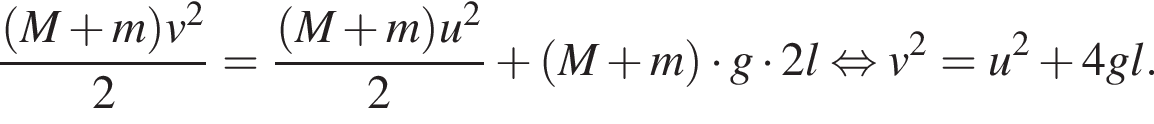
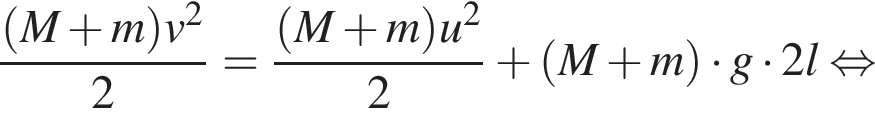
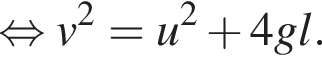
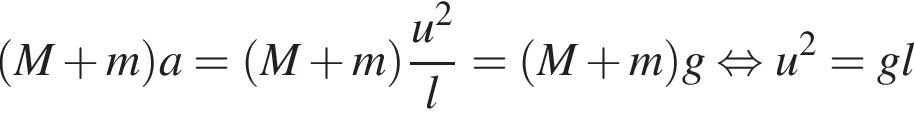
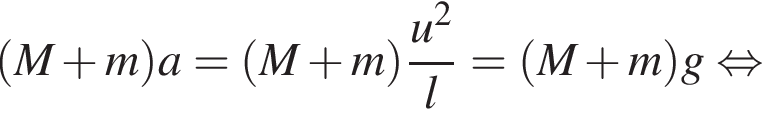
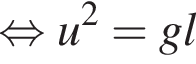
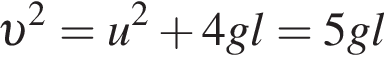
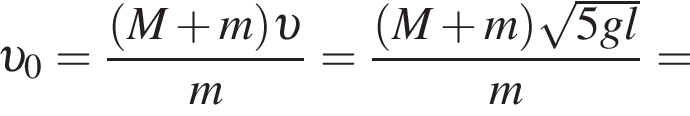
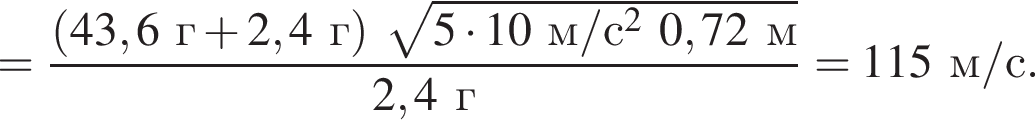
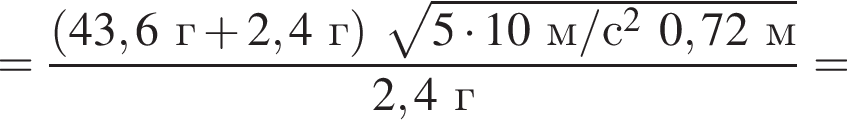
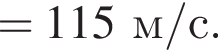
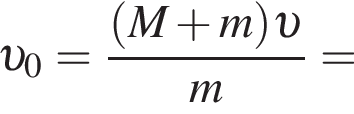
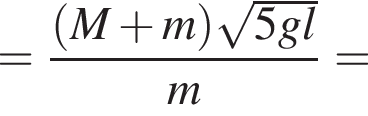
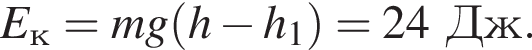
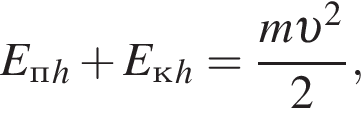 где Eпh − потенциальная энергия на высоте h, Eкh − кинетическая энергия на высоте h, они равны, значит,
где Eпh − потенциальная энергия на высоте h, Eкh − кинетическая энергия на высоте h, они равны, значит, 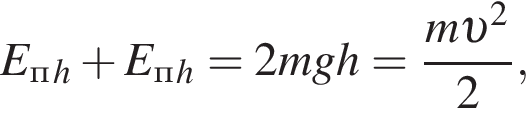 следовательно,
следовательно,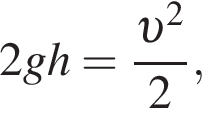
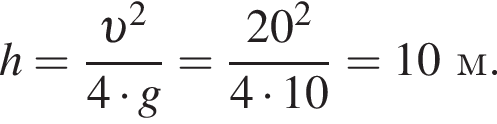
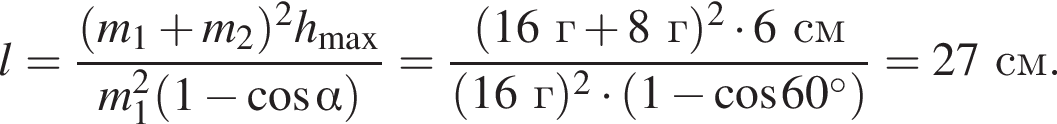
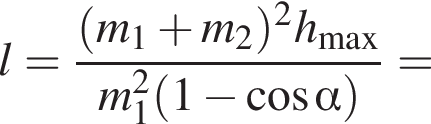
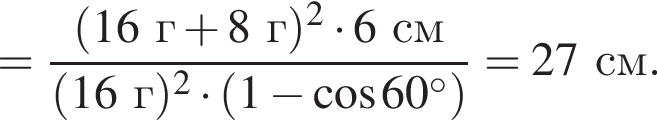
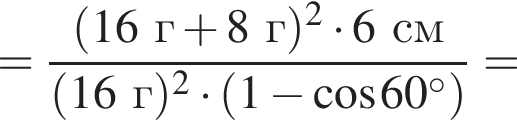
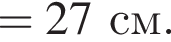
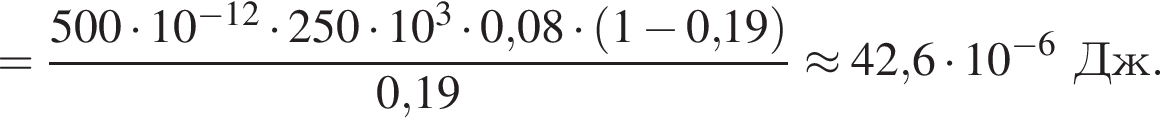
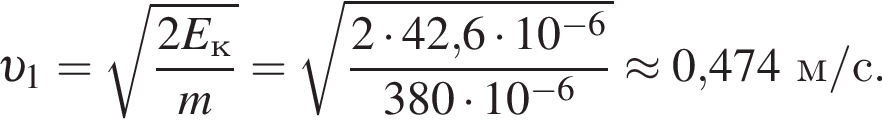
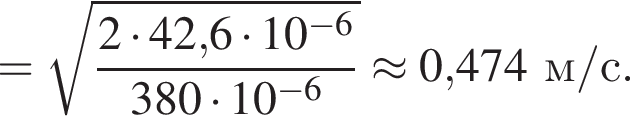
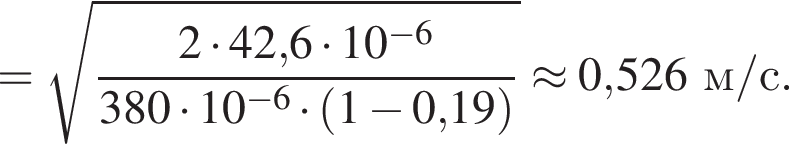
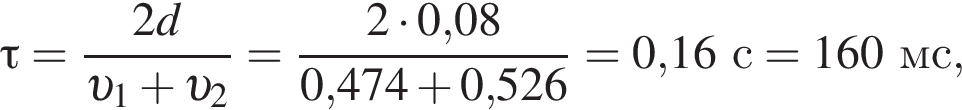
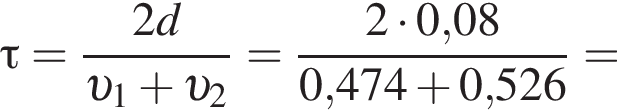
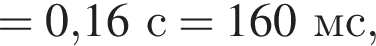
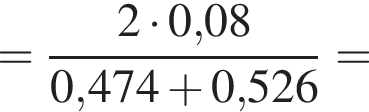

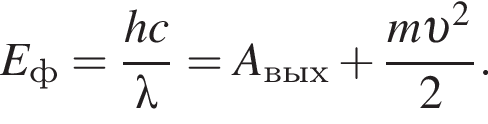
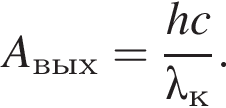
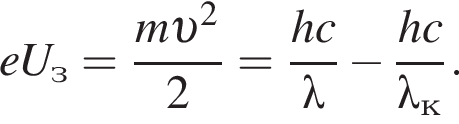
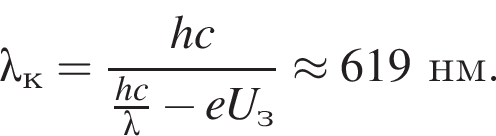

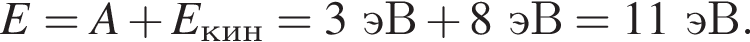
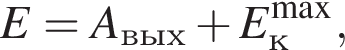 получаем:
получаем: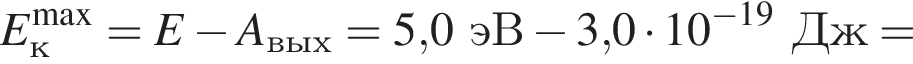
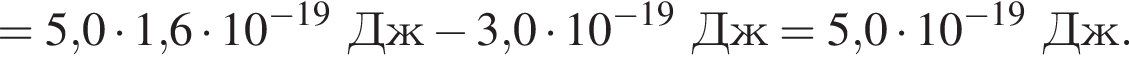
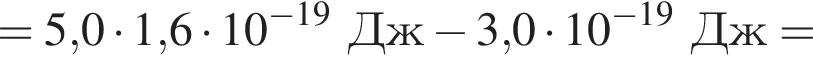
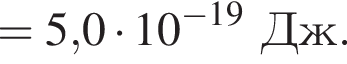
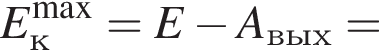
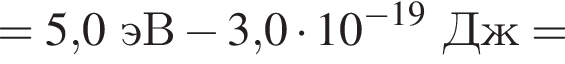
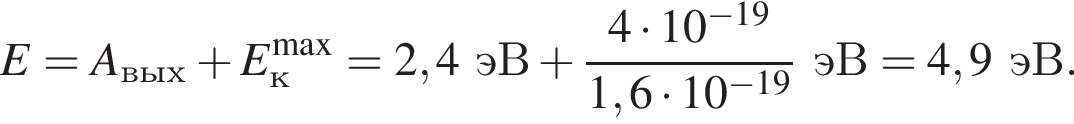
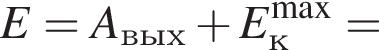
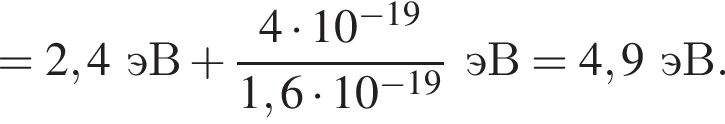
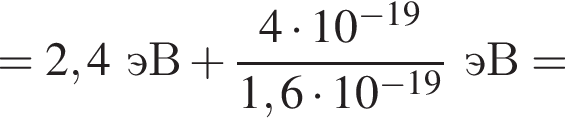
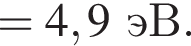
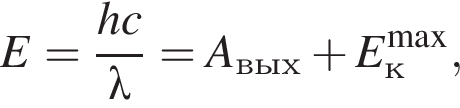 получаем:
получаем: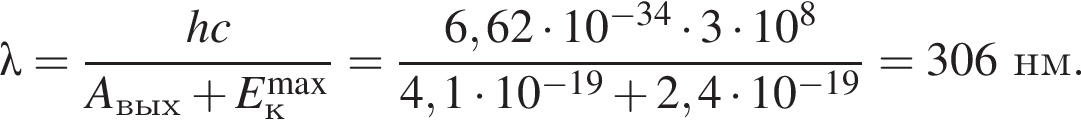
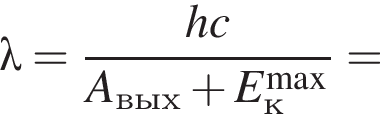
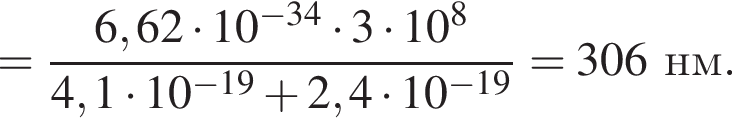
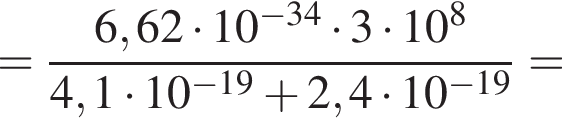


 Амплитудное значение силы тока в
Амплитудное значение силы тока в 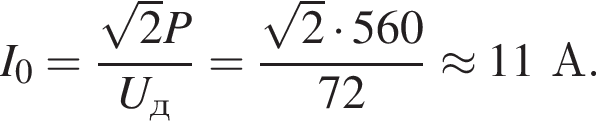
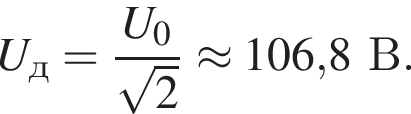 Потребляемая мощность равна:
Потребляемая мощность равна: 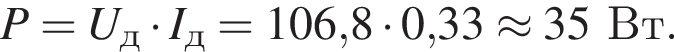
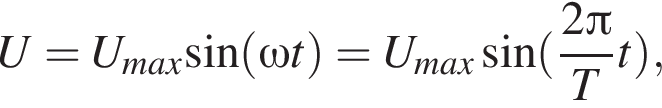
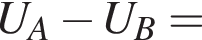
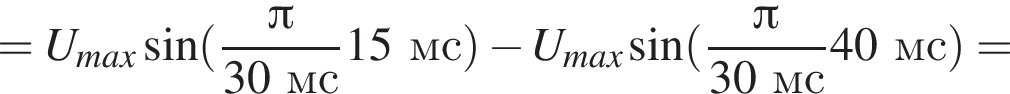
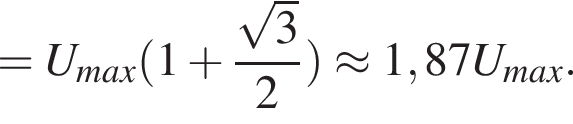
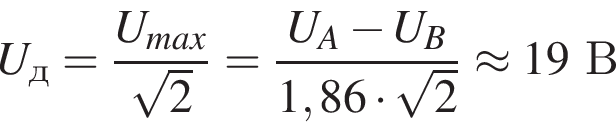
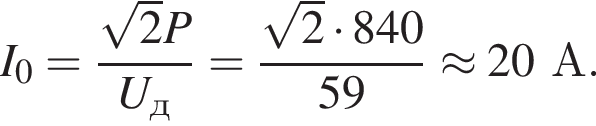
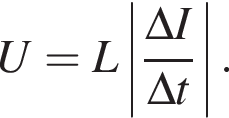 Из графика видно, что наибольшая скорость изменения силы тока на участке BC. Лампочка будет светить наиболее ярко в течение этого интервала времени.
Из графика видно, что наибольшая скорость изменения силы тока на участке BC. Лампочка будет светить наиболее ярко в течение этого интервала времени.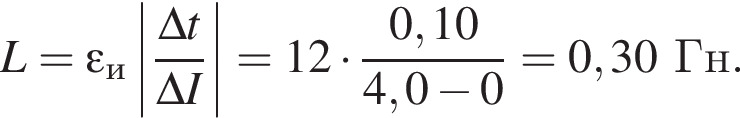
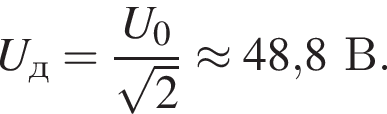 Потребляемая мощность равна:
Потребляемая мощность равна: 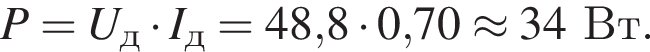
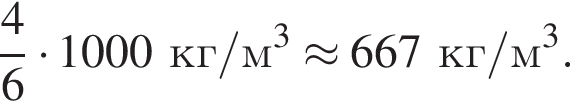 Объём цилиндра равен
Объём цилиндра равен 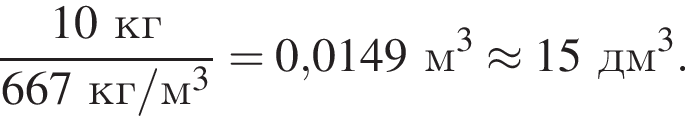
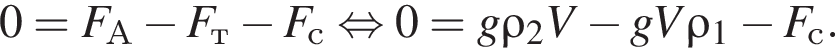
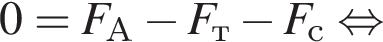
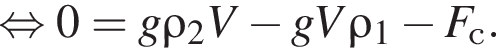
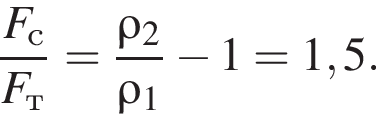
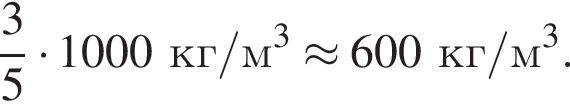 Объём цилиндра равен
Объём цилиндра равен 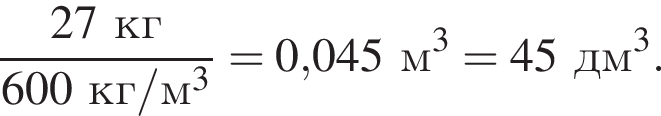
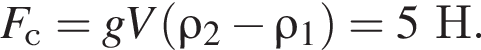

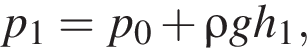
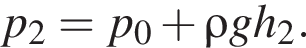
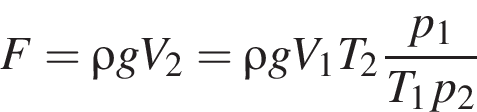
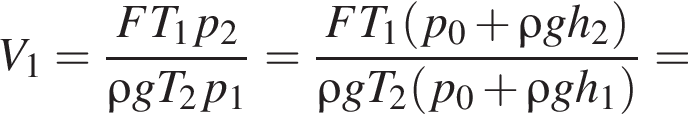
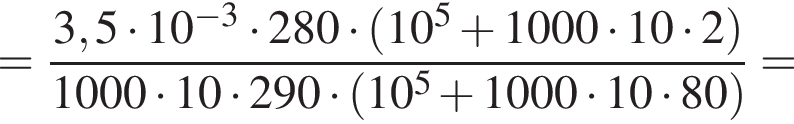
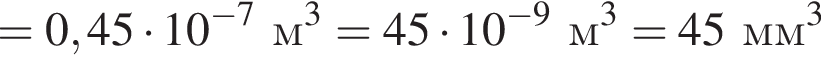
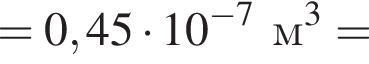
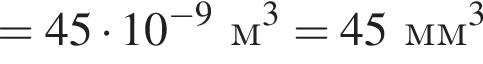
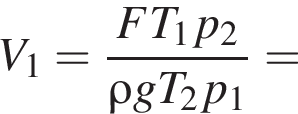
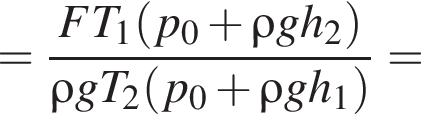
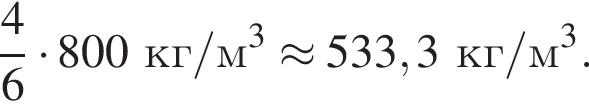 Масса цилиндра равна
Масса цилиндра равна 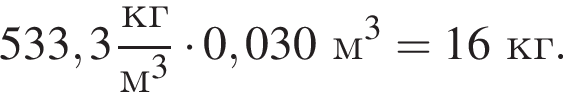
 Объём цилиндра равен
Объём цилиндра равен